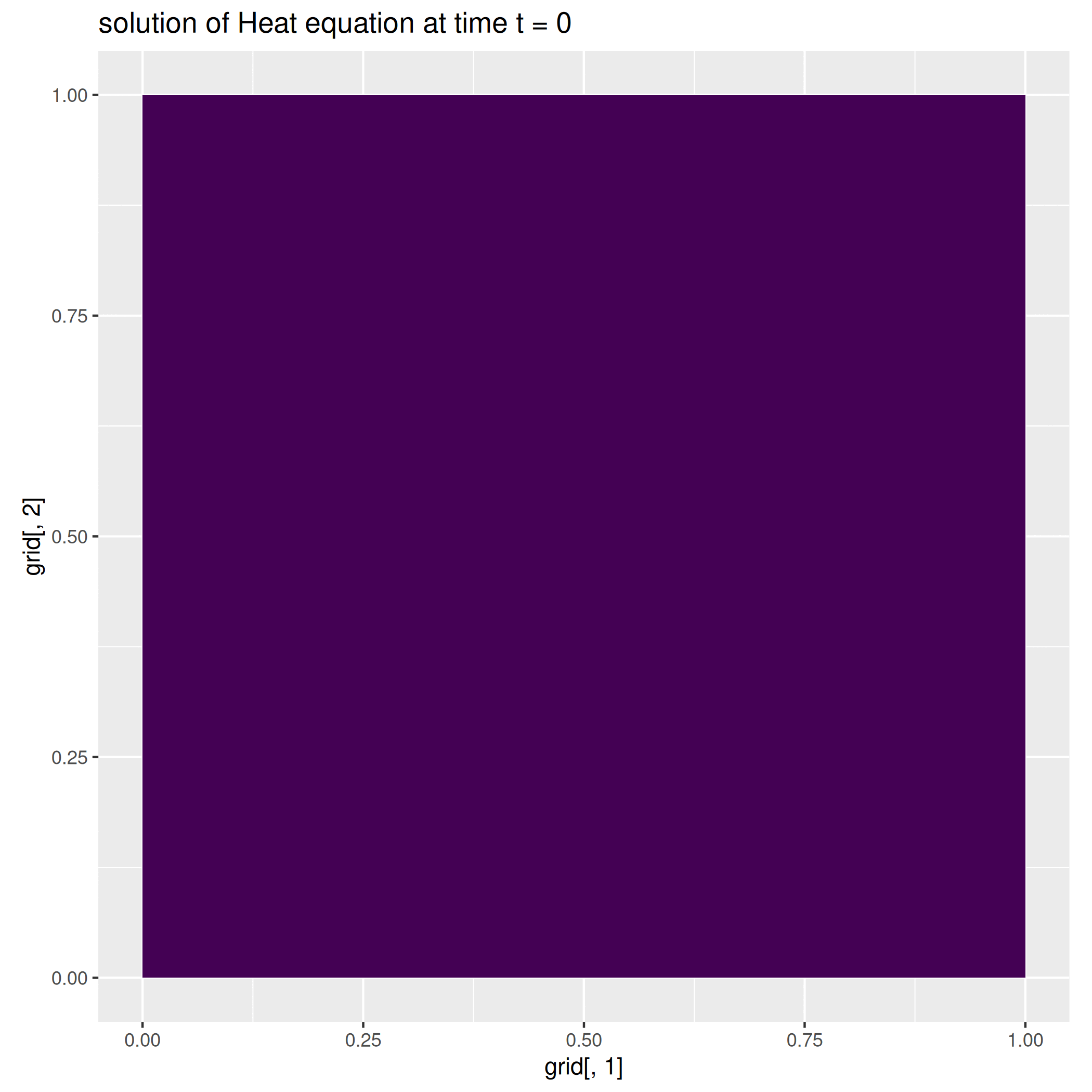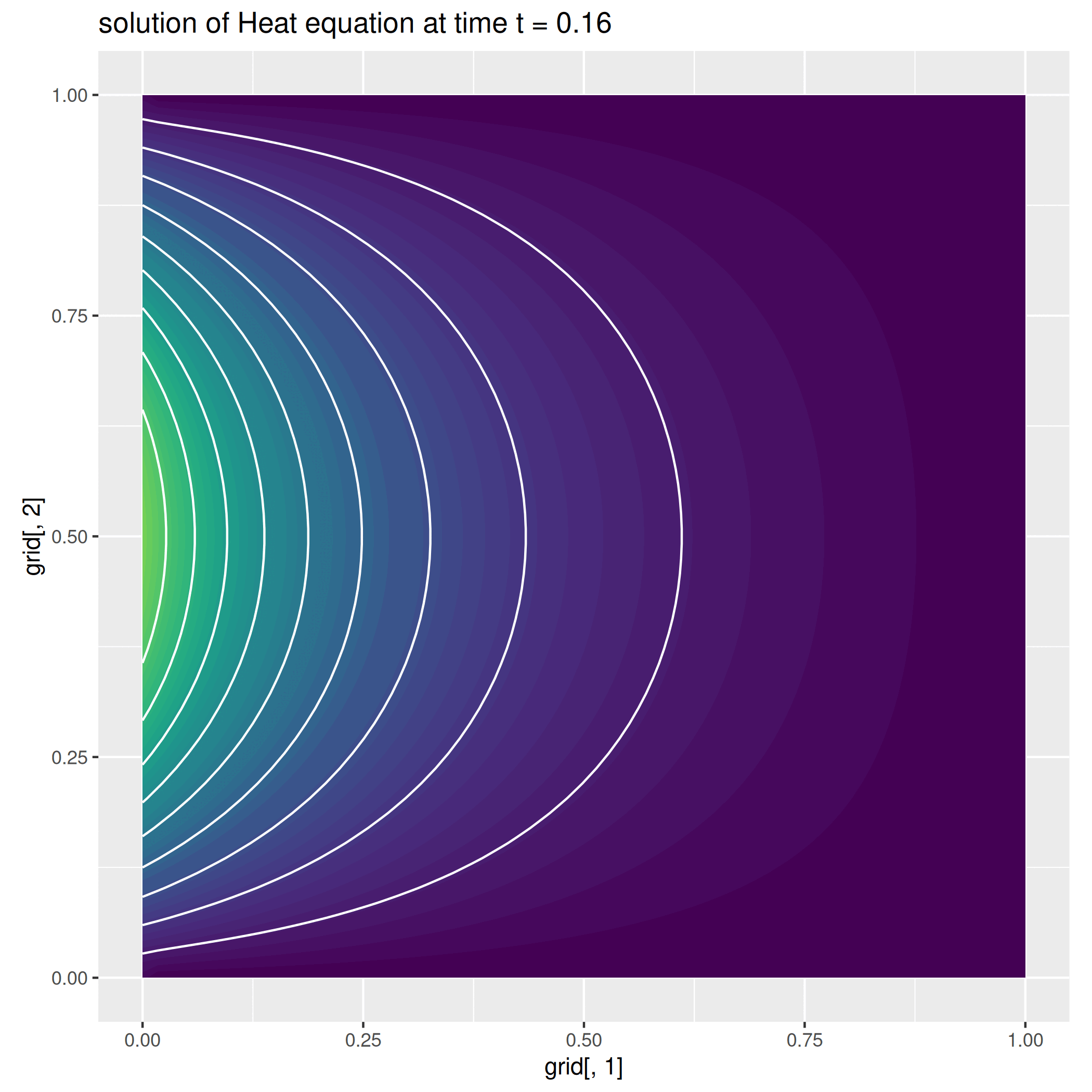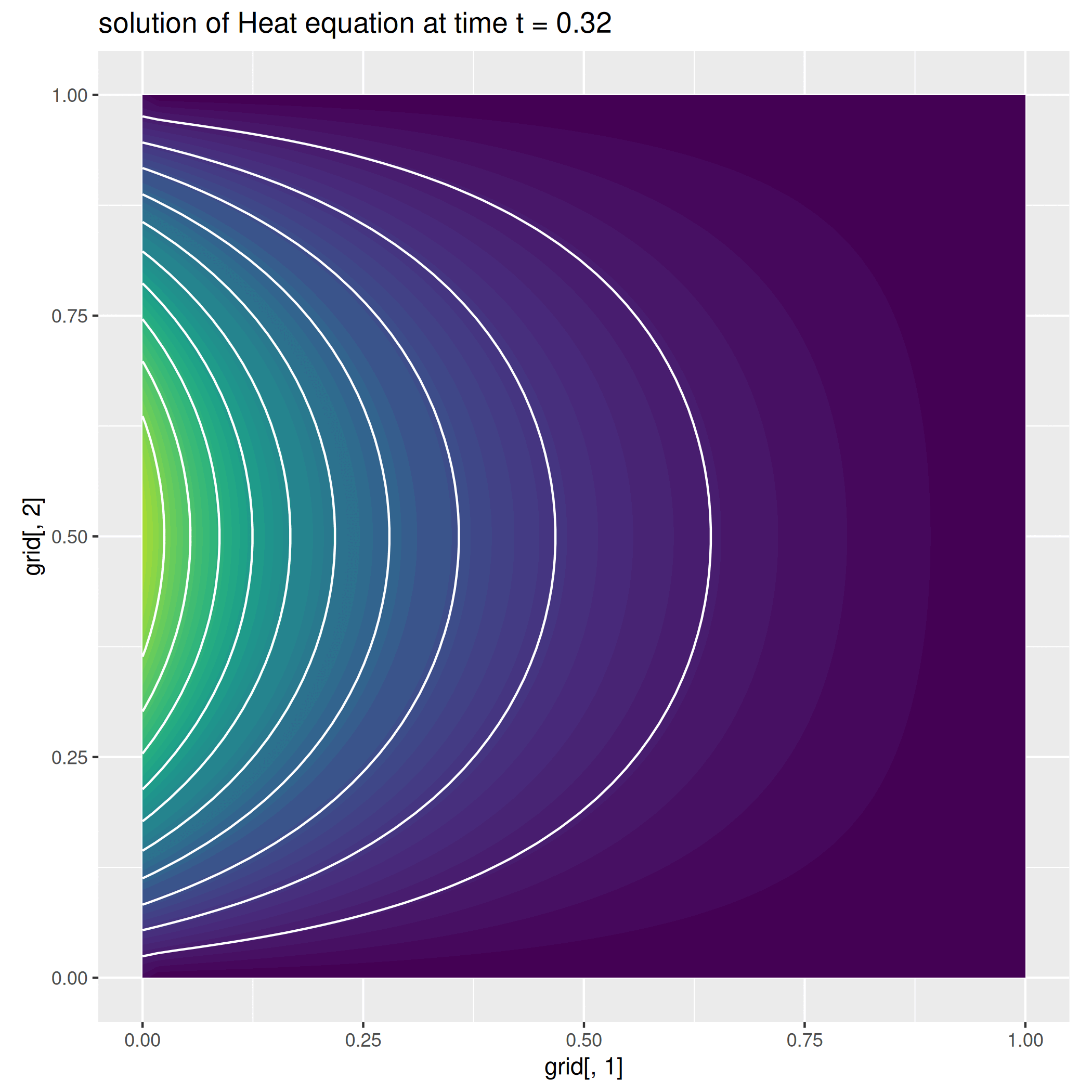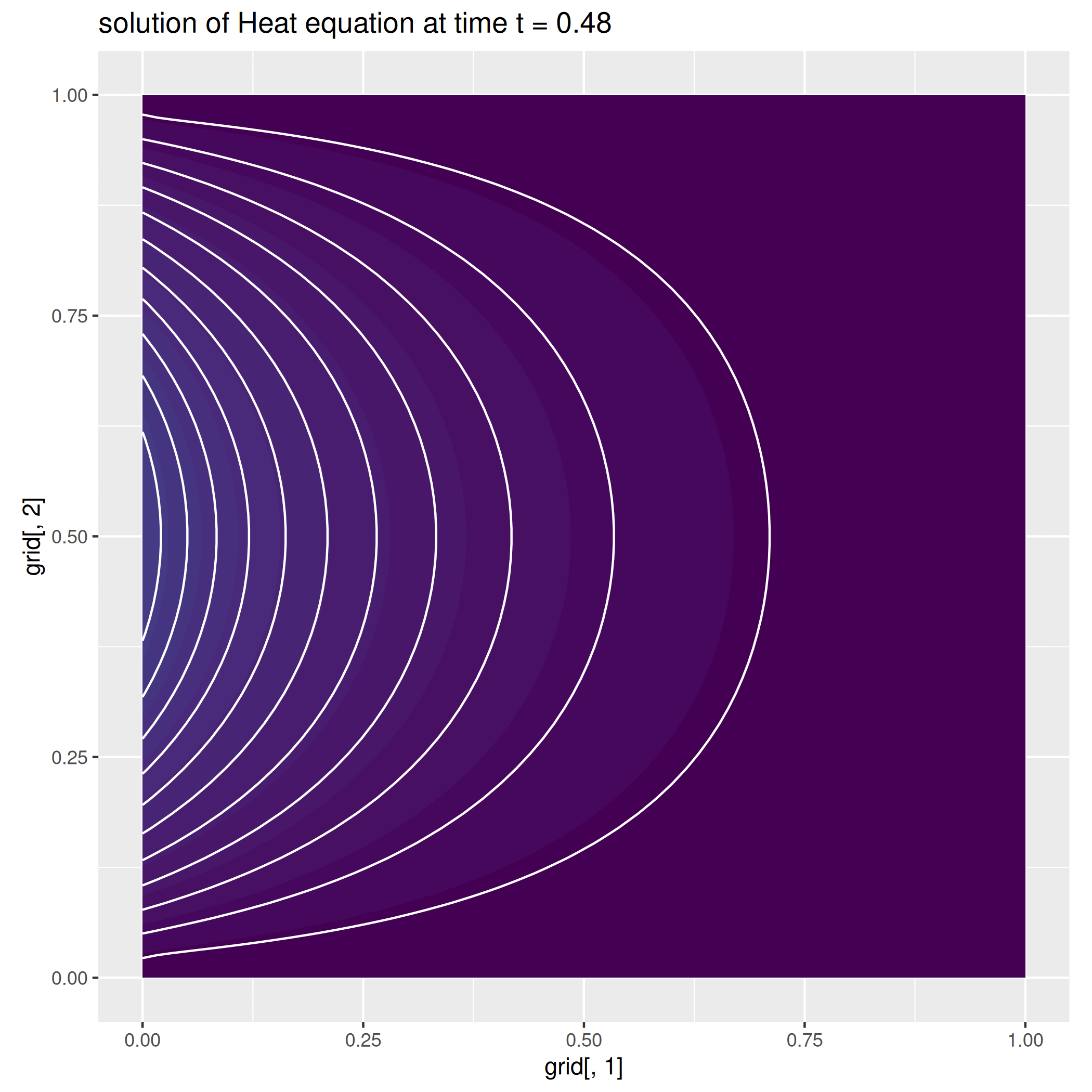
Example 2: The Heat equation¶
In this example we show how to use the fdaPDE-core library to build a numerical scheme for the solution of the heat equation
where \(\Gamma_D, \Gamma_N \in \partial \Omega\) are such that \(\Gamma_D \cup \Gamma_N = \partial \Omega\), \(g_D(\boldsymbol{x}, t), g_N(\boldsymbol{x}, t)\) denote the Dirichlet and Neumann boundary data respectively and \(u_0(\boldsymbol{x})\) represents the given initial condition. \(\boldsymbol{n}\) is the outward normal vector to \(\partial \Omega\).
As always, we start by deriving the weak formulation, by multiplying for each \(t > 0\) the differential equation by a test function \(v \in V = H^1_{\Gamma_D}(\Omega)\) and integrating on the spatial domain only \(\Omega\). Specifically, for each \(t > 0\) we seek \(u(t) \in V\) such that
Integrating by parts the Laplacian leads to the weak formulation
As usual, the Galerkin approach considers a finite dimensional space \(V_h \subset V\) and writes \(u(\boldsymbol{x}, t) = \sum_{j=1}^N u_j(t) \psi_j(\boldsymbol{x})\). Substituting in the weak formulation, computations lead to the following semi-discretization
Let \(M = [m_{ij}] = \int_{\Omega} \psi_i \psi_j\) be the mass matrix, \(A = [a_{ij}] = \int_{\Omega} \nabla \psi_i \cdot \nabla \psi_j\) be the stiff matrix and \(\boldsymbol{F}(t) = \int_{\Omega} f(\boldsymbol{x}, t) \psi_j(\boldsymbol{x}) + \int_{\Gamma_N} g(\boldsymbol{x}, t) \psi_i(\boldsymbol{x})\) the discretization of the righ hand side of the above relation, we are asked to solve in \(\boldsymbol{u}(t)\) the following systems of ODEs
We decide to solve it via the Crank-Nicolson method, which is a second order method in the time step size \(\Delta t\). Specifically we get
The above is solved iteratively for all the time steps \(k = 1, \ldots, N_T\).
Implementation¶
For the first example we consider homogeneous Neumann and Dirichlet conditions on the domain boundary and a space-time depending forcing term. We initially define the geometry, togheter with a finite element space and the definition of bilinear form of the laplace operator (observe that (the bilinear form of) any elliptic operator could have been placed here, in case of general parabolic equations).
Triangulation<2, 2> unit_square = Triangulation<2, 2>::UnitSquare(60, cache_cells);
FeSpace Vh(unit_square, P1<1>); // piecewise linear continuous scalar finite elements
TrialFunction u(Vh);
TestFunction v(Vh);;
// laplacian operator bilinear form
auto a = integral(unit_square)(dot(grad(u), grad(v)));
We then define the forcing term. Because we are dealing with a space-time problem, we use the specialized SpaceTimeField type, which extends the ScalarField capabilities to handle an explicit time coordinate. Specifically, the code below implements the forcing term
// define forcing functional
SpaceTimeField<2, decltype([](const PointT& p, double t) {
if (p[0] < 0.5 && p[1] < 0.5 && t >= 0.0 && t <= 0.2) {
return 1;
} else if (p[0] > 0.5 && p[1] > 0.5 && t >= 0.2 && t <= 0.4) {
return 1;
} else {
return 0;
}
})> f;
You can fix the time coordinate calling f.at(t). Subsequent calls of f at a spatial point will act as calls to a ScalarField where the time coordinate has been fixed to t. Next we proceed to fix homogeneous boundary conditions on all the domain’s boundary
ScalarField<2, decltype([](const PointT& p) { return 0; })> g;
auto& dof_handler = Vh.dof_handler();
dof_handler.set_dirichlet_constraint(/* on = */ BoundaryAll, /* data = */ g);
Finally, we fix the time step \(\Delta t\), set up room for the solution fixing the initial condition to \(u_0(\boldsymbol{x}) = 0\) and discretizing once and for all the mass matrix \(M\) and the stiff matrix \(\frac{M}{\Delta T} + \frac{1}{2} A\), togheter with the forcing term \(F(t)\). Since the matrix \(\frac{M}{\Delta T} + \frac{1}{2} A\) is SPD and time-invariant, we factorize it outside the time integration loop using a Cholesky factorization:
Eigen::SparseMatrix<double> M = integral(unit_square)(u * v).assemble(); // mass matrix
Eigen::SparseMatrix<double> A = M / DeltaT + a.assemble() * 0.5; // stiff matrix (SPD)
// discretize time-dependent forcing field
Eigen::Matrix<double, Dynamic, Dynamic> F(dof_handler.n_dofs(), n_times);
for (int i = 0; i < n_times; ++i) { F.col(i) = integral(unit_square)(f.at(DeltaT * i) * v).assemble(); }
dof_handler.enforce_constraints(A); // set dirichlet constraints
Eigen::SimplicialLLT<Eigen::SparseMatrix<double>> lin_solver(A);
Finally, the crank-nicolson time integration loop can start:
for (int i = 1; i < n_times; ++i) {
Eigen::Matrix<double, Dynamic, 1> b =
(M / DeltaT - A / 2) * solution.col(i - 1) + 0.5 * (F.col(i) + F.col(i - 1)); // update rhs
dof_handler.enforce_constraints(b);
solution.col(i) = lin_solver.solve(b);
}
The complete script
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | |
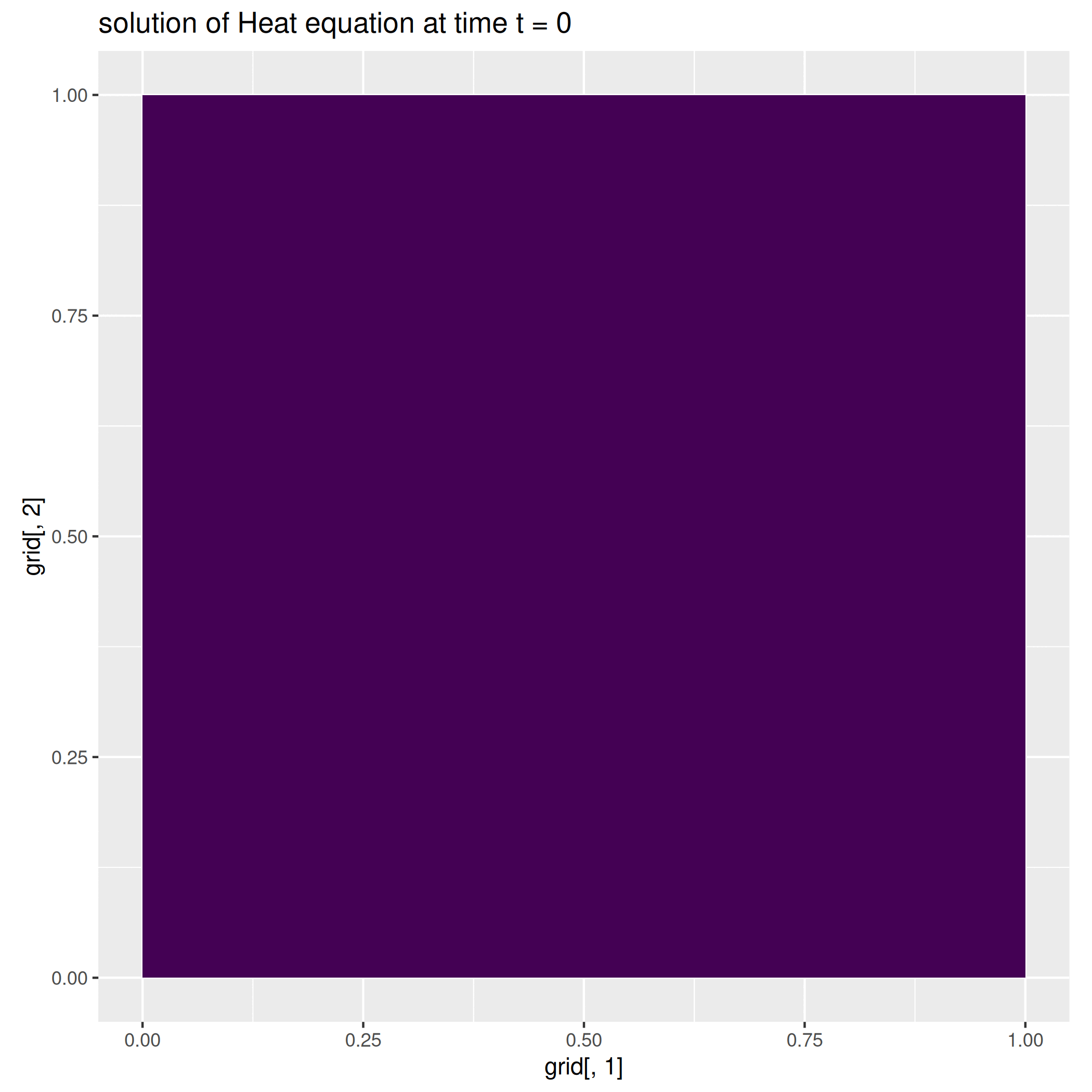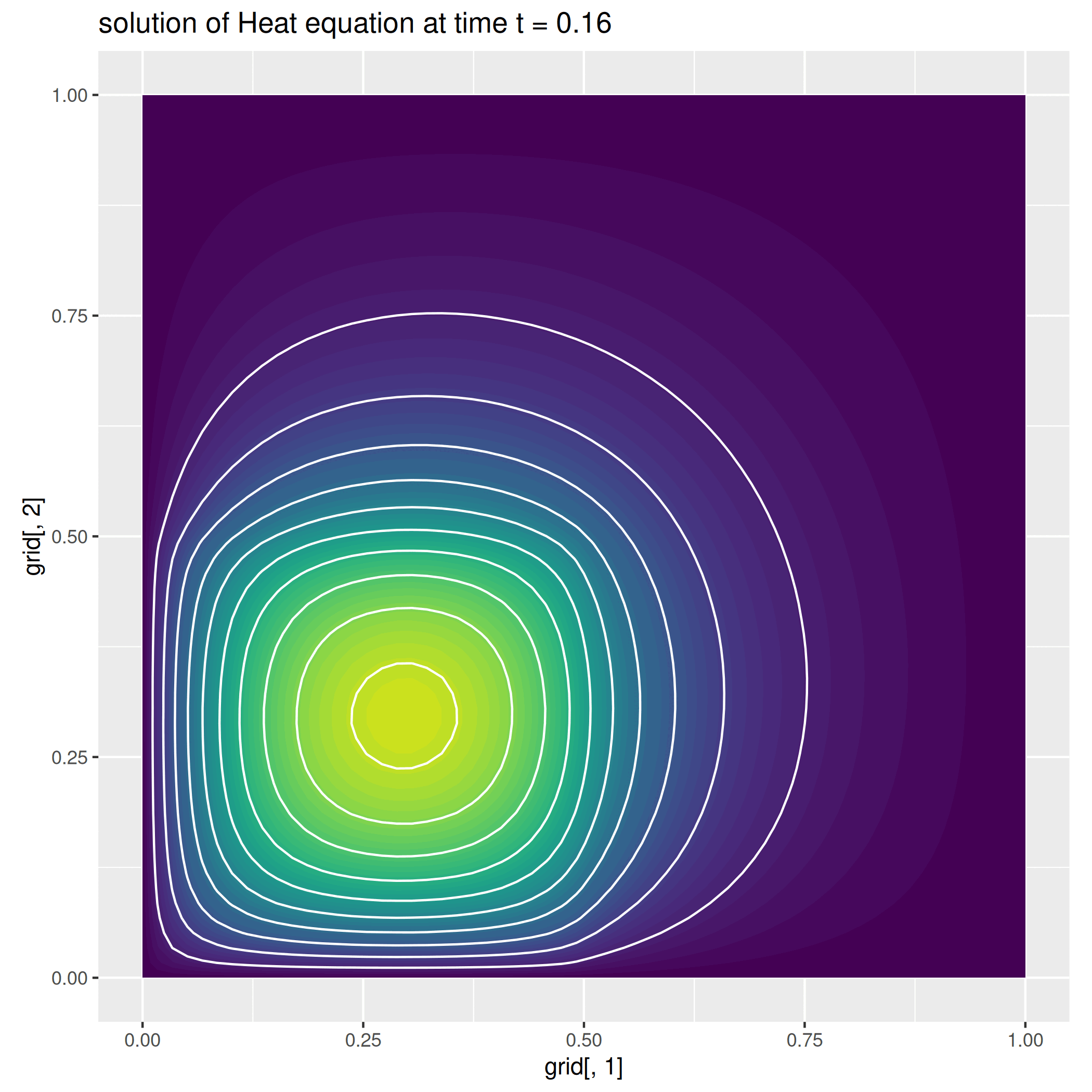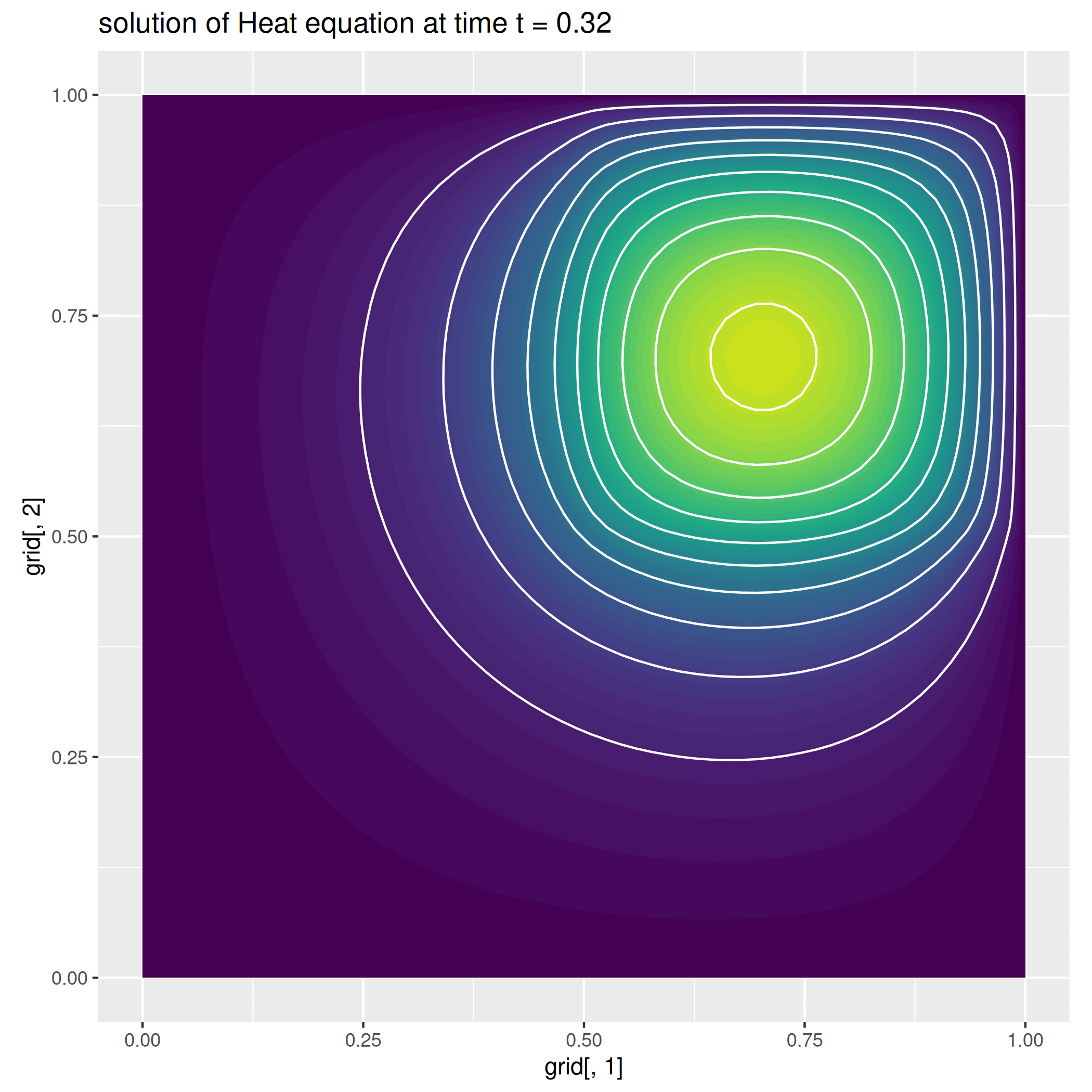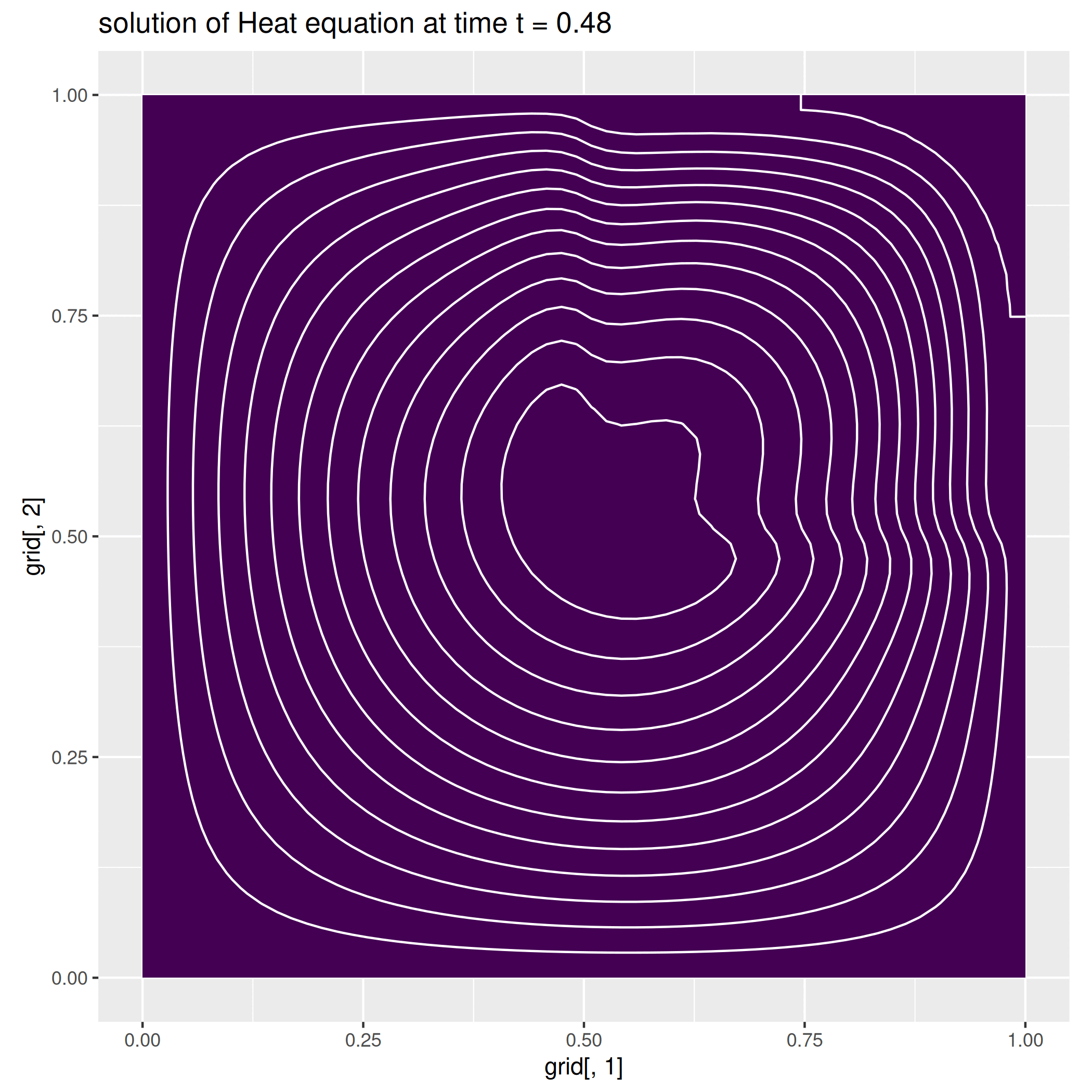
We here report a slight variation of the problem above, where we consider a null-forcing term, but a non-homogeneous time-dependent Neumann condition on the left side of the square, while we impose a zero dirichlet condition on the remaining part of the boundary.
Tip
We pose the attention on the mechanism which enables us to define the different portions of the domain’s boundary \(\Gamma_D\) and \(\Gamma_N\). Specifically, every boundary element of the geometry can be associated to a numerical non-negative marker, so that, boundary elements with the same marker contributes to the definition of the same boundary subset \(\Gamma \subset \partial \Omega\).
Each Triangulation object starts with an empty set of boundary markers (in this case, we name the boundary elements which have no marker as Unmarked). You can fix a value for the boundary markers using the mark_boundary() method of a Triangulation instance. For instance, to fix all the markers of the triangulation to 0, just use
unit_square.mark_boundary(/* as = */ 0); // mark all nodes as zero
You can use a geometric predicate to obtain a more selective marking. In the considered example, we can mark only the left side of the unit square \([0,1]^2\) by setting the marker of all the edges on the left side to 1 using the following
unit_square.mark_boundary(/* as = */ 1, /* where = */ [](const typename Triangulation<2, 2>::EdgeType& edge) {
return (edge.node(0)[0] == 0 && edge.node(1)[0] == 0); // select only edges on the left side
});
Be aware that markers with higher values have higher precedence on markers with lower values, that is, markers with higher values will overwrite existing markers with lower values, the viceversa is not true.
Once you have fixed the markers, you can iterate on all the boundary elements having a fixed marker using the overload of the boundary_begin() and boundary_end() methods taking the marker as parameter. For instance, to iterate over \(Gamma_N\) only (assuming being identified with marker 1) you execute:
for(auto it = unit_square.boundary_begin(1); it != unit_square.boundary_end(1); ++it) {
// all and only the boundary edges marked as 1
}
The script is mostly similar to the Crank-Nicolson time-stepping scheme implemented before, apart for the definition of the boundary conditions and the introduction of the non-homogeneous neumann boundary term at line 46
integral(unit_square.boundary(/* on = */ 1))(g_N.at(DeltaT * i) * v)
The complete script
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | |