Example 3: SUPG for advection dominated equations¶

In this tutorial we consider a second order diffusion-transport-reaction equation

\[\begin{split}\begin{align} - \mu \Delta u + \langle b, \nabla u \rangle + u = f & \qquad \text{in } \Omega \\ u = g & \qquad \text{on } \partial \Omega \end{align}\end{split}\]

with \(\Omega = [0,1]^2\) and assuming an advection-dominated regime. Specifically, we set the diffusion coefficient \(\mu = 10^{-5}\) and we take a non-constant transport field \(b : \Omega \rightarrow \mathbb{R}^2\) given by the equation

\[\begin{split}b = \begin{bmatrix} 2 y^2 + 1 \\ 2 x \end{bmatrix}.\end{split}\]

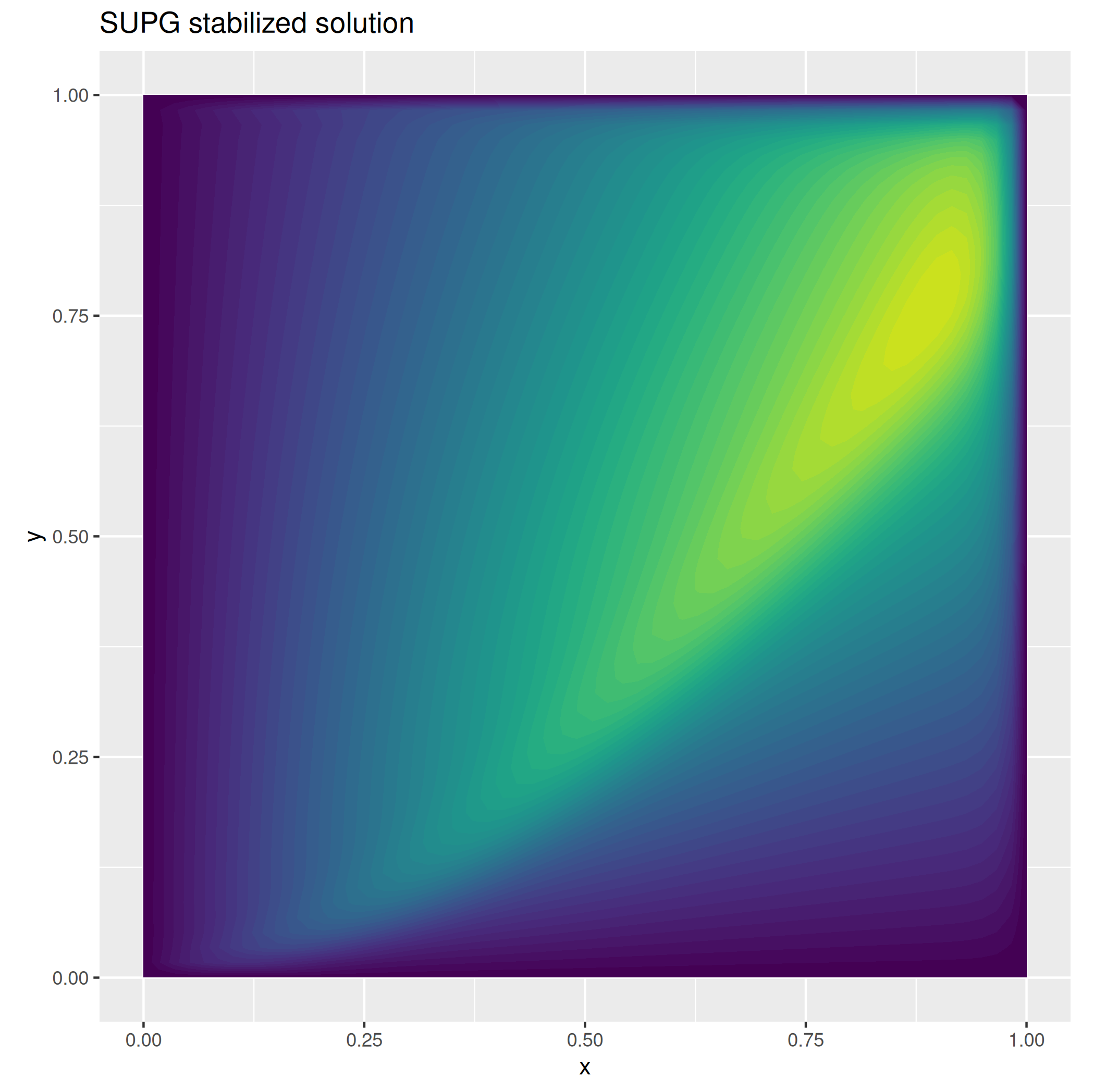
The boundary conditions are set Dirichlet homogeneous over all domain boundary, i.e. \(g = 0\). As the Peclet number results bigger than one, numerical stabilization techniques are required to avoid spurious ossilations in the solution. We here analyze the Streamline Upwind Petrov–Galerkin (SUPG) approach, a strongly consistent stabilization method, togheter with its C++ implementation using the C++ fdaPDE-core API.

Let \(V\) be a proper Sobolev space where the solution has to be searched. Define \(a(u, v) = \int_{\Omega} \mu \nabla u \cdot \nabla v + \langle b, \nabla u \rangle v + uv\) the bilinear form associated to the weak formulation of the considered problem, and let \(F(v) = \int_{\Omega} fv\) be the corresponding linear form. Following the usual Galerkin approach, we consider a family of finite dimensional subspaces \(V_h\) of \(V\) and search \(u_h \in V_h\) such that \(a(u_h, v_h) = F(v_h)\) for any \(v_h \in V_h\). Due to the finite-dimensional nature of \(V_h\), the problem is typically reduced to solving a linear system. However, in case of advection dominated problems, the direct solution of such linear system results in numerical instabilities. SUPG instead seeks a solution \(u_h \in V_h\) such that

\[a(u_h, v_h) + \sum_{k \in T_h} \tau_k \langle Lu_h, b \cdot \nabla v_h \rangle_{L^2(\Omega)} = F(v_h) + \sum_{k \in T_h} \tau_k f (b \cdot \nabla v_h) \quad \forall v_h \in V_h\]

where \(T_h\) is a discretization of the problem domain \(\Omega\), \(Lu_h\) is the PDE in strong formulation and \(\tau_k\) is a suitably choosen stabilization parameter. The latter is tipically parametrized as follow \(\delta \frac{h_k}{2 \| b \|_2}\), where \(\delta\) is a problem dependent parameter and \(h_k\) denots the characteristic length (i.e. the diameter) of the \(k\)-th cell of \(T_h\).

As such, define the bilinear form

\[\tilde a(u_h, v_h) = \int_{\Omega} \bigl[ \mu \nabla u_h \cdot \nabla v_h + \langle b, \nabla u_h \rangle v_h + u_h v_h \bigr] + \sum_{k \in T_h} \tau_k (- \mu \Delta u_h + \langle b, \nabla u_h \rangle + u_h) (b \cdot \nabla v_h)\]

and the linear form

\[\tilde F(v_h) = \int_{\Omega} fv_h + \sum_{k \in T_h} \tau_k f (b \cdot \nabla v_h)\]

then we are required to find \(u_h \in V_h\) solution of \(\tilde a(u_h, v_h) = \tilde F(v_h)\) for all \(v_h \in V_h\). Using the standard Galerkin argument, we are left to the solution of a linear system resulting from the discretization of \(\tilde a(u_h, v_h)\) and \(\tilde F(v_h)\).

Implementation¶

As usual, we start by creating the geometry and the finite element space, togheter with trial and test functions. We also define the non-constant transport field \(b\) as a MatrixField

Triangulation<2, 2> unit_square = Triangulation<2, 2>::UnitSquare(60, cache_cells);

FeSpace Vh(unit_square, P1<1>);   // piecewise linear continuous scalar finite elements
TrialFunction u(Vh);
TestFunction  v(Vh);

// transport field
MatrixField<local_dim, local_dim, 1> b;
b[0] = [](const PointT& p) { return std::pow(p[1], 2) + 1; };
b[1] = [](const PointT& p) { return 2 * p[0]; };
// diffusion coefficient
double mu = 1e-5;

// forcing term
ScalarField<2, decltype([](const PointT& p) { return 1; })> f;

Secondly, we instantiate the integration loops for the bilinear form \(a(u,v)\) and the linear functional \(F(v)\) without SUPG correction

auto a = integral(unit_square)(mu * dot(grad(u), grad(v)) + dot(b, grad(u)) * v + u * v);
auto F = integral(unit_square)(f * v);

Info

You don’t have to care about the fact that \(b\) is not a constant. The integrator loops will recognize this fact and silently perform the required actions (i.e., distribute the quadrature nodes on the physical domain and evaluate non-constant coefficients at them) in order to perform the discretization.

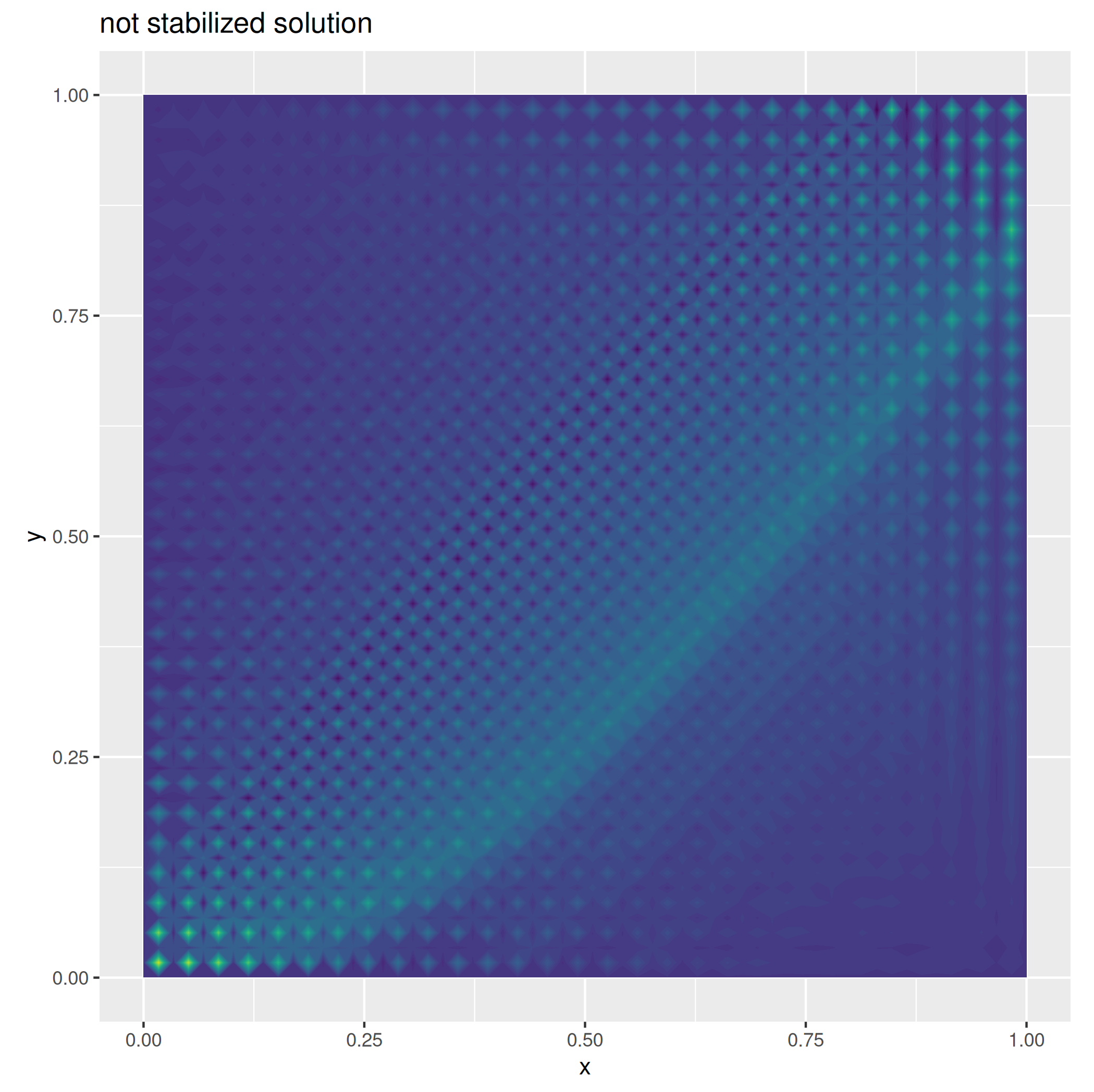
We might observe that solving the linear system resulting from the discretization of a and F alone will result in an unstable solution, as shown in the figure below.

In order to apply SUPG, let us first define the stabilization parameter \(\tau_k\) and observe that this depends on the cell diameter \(h_k\). As such, \(\tau_k\) will not be a constant during the integration loop. The type CellDiameterDescriptor can be used as a placeholder inside an expression to denote \(h_k\). During the integration loop, the integrator will take care to substitute, cell by cell, \(h_k\) with its actual numerical value.

CellDiameterDescriptor h_k(unit_square);
double delta = 2.85;
double b_norm = integral(unit_square, QS2DP2)(b.norm());   // transport field norm

auto tau_k  = 0.5 * delta * h_k / b_norm;   // stabilization parameter

Info

We can compute the integral of any expression using the integral interface. Provided that the expression does not involve any trial nor test function, integral(D)(f) will return the numerical value (as double) of \(\int_D f\). A quadrature rule is mandatory in this case, as the code cannot deduce any valid quadrature rule from f alone.

In case the domain of integration D is a triangulation, only simplex quadrature formulas of the QS family are accepted, in which case the integration is performed as

\[\int_D f = \sum_{k \in T_h} \int_k f \approx \sum_{k \in T_k} \sum_{q} w_q f(x_q).\]

The line of code

double b_norm = integral(unit_square, QS2DP2)(b.norm());

in the definition of the stablization parameter computes \(\int_{[0,1]^2} \| b \|_2\) using a two dimensional 3 point simplex rule (QS2DP2).

We have now all the ingredients to assemble the stabilized bilinear forms \(\tilde a(u,v)\) and \(\tilde F(v)\):

auto a_supg =
    a + integral(unit_square)(tau_k * (-mu * (dxx(u) + dyy(u)) + dot(b, grad(u)) + u) * dot(b, grad(v)));
auto F_supg = F + integral(unit_square)(tau_k * f * dot(b, grad(v)));

Info

The laplace operator in strong form is implemented using second derivative accessors dxx() and dyy(). In case of P1 finite elements (or any finite element description whose second derivative is zero), those functions immediately returns 0 and are therefore completely optimized out during the assembly phase.

Upon discretization and imposition of boundary conditions, the solution of the discretized linear system provides us with a stabilized solution.

The complete script

#include <fdaPDE/finite_elements.h>
using namespace fdapde;

int main() {
   // useful typedef and constants definition
   constexpr int local_dim = 2;
   using PointT = Eigen::Matrix<double, local_dim, 1>;

   Triangulation<local_dim, local_dim> unit_square = Triangulation<2, 2>::UnitSquare(60, cache_cells);

   FeSpace Vh(unit_square, P1<1>);
   TrialFunction u(Vh);
   TestFunction  v(Vh);
   // transport field
   MatrixField<local_dim, local_dim, 1> b;
   b[0] = [](const PointT& p) { return std::pow(p[1], 2) + 1; };
   b[1] = [](const PointT& p) { return 2 * p[0]; };
   // diffusion coefficent
   double mu = 1e-5;
   // forcing term
   ScalarField<local_dim, decltype([](const PointT& p) { return 1; })> f;

   // not stabilized forms
   auto a = integral(unit_square)(mu * dot(grad(u), grad(v)) + dot(b, grad(u)) * v + u * v);
   auto F = integral(unit_square)(f * v);

   // SUPG correction
   CellDiameterDescriptor h_k(unit_square);
   double delta = 2.85;
   double b_norm = integral(unit_square, QS2DP2)(b.norm());   // transport field norm
   auto tau_k  = 0.5 * delta * h_k / b_norm;   // stabilization parameter
   auto a_supg = a + integral(unit_square)(tau_k * (-mu * (dxx(u) + dyy(u)) + dot(b, grad(u)) + u) * dot(b, grad(v)));
   auto F_supg = F + integral(unit_square)(f * v + tau_k * f * dot(b, grad(v)));

   // homogeneous dirichlet data
   ScalarField<local_dim, decltype([](const PointT& p) { return 0; })> g;
   auto& dof_handler = Vh.dof_handler();
   dof_handler.set_dirichlet_constraint(/* on = */ BoundaryAll, /* data = */ g);
   // discretization
   Eigen::SparseMatrix<double> A = a_supg.assemble();
   Eigen::Matrix<double, Dynamic, 1> B = F_supg.assemble();
   dof_handler.enforce_constraints(A, B);
   // solve step
   Eigen::SparseLU<Eigen::SparseMatrix<double>> solver(A);
   Eigen::Matrix<double, Dynamic, 1> solution = solver.solve(B);

   return 0;
}