Alpha testing fdaPDE 2.0 [cpp]¶

Cari tutti, benvenuti nella pagina di alpha-testing di fdaPDE 2.0. Scopo di questo documento è quello di mostrare quanto sia semplice tradurre uno script R o cpp, scritto per una qualunque versione precedente della libreria, usando la nuova API di fdaPDE.

Lo scopo della fase di testing è quello di rompere la libreria, e, tra le altre cose, di stressarmi. Pertanto:

• se trovate bug (il codice crasha, il codice non compila, i numeri sono sbagliati, …)

• se trovate qualcosa di poco intuitivo

• se mancano pezzi, rispetto alla libreria attualmente su CRAN, o rispetto a lavoro pregresso che avete fatto ma che non trovate nel codice attuale

• se volete aggiungere delle modelistiche che state ora sviluppando o funzionalità che trovate interessanti

segnalatemelo (mi scrivete su whatsapp o me lo dite di persona).

How to fdaPDE¶

L’idea generale è quella di scrivere degli script, che vedono fdaPDE come una libreria terza. Quindi, create un bel file main.cpp, fuori dalla cartella dove avete il sorgente di fdaPDE, e per iniziare scrivete quanto segue:

1
2
3
4
5
6
7
8
9

#include <fdaPDE/models.h> // include the whole library
using namespace fdapde;

int main() {

    // codice di test

    return 0;
}

La libreria è composta da diversi moduli. Il modo più semplice per avere un ambiente funzionante è quello di caricare l’header <fdaPDE/models.h>, il quale, attualmente, carica tutto lo stack della libreria. Per convenienza, importiamo anche il namespace fdapde.

Per compilare, al momento, solo gcc14 (o superiore) è supportato. Usate la seguente riga di codice (supponendo di essere nella cartella test/mio_test):

g++ -o main main.cpp -I../../fdaPDE-cpp -I../../fdaPDE-cpp/fdaPDE/core -O2 -march=native -std=c++20 -s

Tipicamente, l’anatomia di uno script è la seguente:

1. definizione della geometria: il primo step è quello di definire la geometria del problema. In questa fase tratteremo unicamente discretizzazioni agli elementi finiti, e pertanto le nostre geometrie saranno unicamente triangolazioni. Potete caricare una triangolazione con il seguente codice:

1
2
3

Triangulation<2, 2> D(
    "mesh/nodes.csv", "mesh/cells.csv", "mesh/boundary.csv",
    /* header = */ true, /* index_col = */ true);

Alternativamente, potete generare delle semplici geometrie in maniera dinamica nel modo seguente:

1
2
3
4

Triangulation<1, 1> D = Triangulation<1, 1>::UnitInterval(n); // unit interval with n nodes
Triangulation<2, 2> D = Triangulation<2, 2>::UnitSquare(n);   // unit square with n nodes per side
Triangulation<2, 3> D = Triangulation<2, 3>::UnitSphere(n);   // unit sphere surface using n refinments
Triangulation<3, 3> D = Triangulation<3, 3>::UnitCube(n);     // unit cube with n nodes per side

2. definizione dei dati: una volta definita la geometria, possiamo caricare i dati. A tal scopo un oggetto di tipo GeoFrame modelizza un data frame per dati che sono spazialmente localizzati su una geometria. Potete definire un GeoFrame nel modo seguente:

1

GeoFrame data(D);

L’oggetto data appena costruito è un GeoFrame definito su una triangolazione D, che rappresenta lo spazio fisico dove sono definiti i dati di interesse. data così costruito non ha alcun dato associato.

Prima di procedere, è bene sapere che GeoFrame è una struttura dati abbastanza complessa. Nella sua interezza, essa rappresenta una struttura multi-layer, ovvero una struttura in grado di gestire dati osservati potenzialmente su supporti differenti.

Tip

Potete immaginare un GeoFrame come una pila dove, alla base, abbiamo un layer fisico definito dalla geometria, sulla quale definiamo uno o più layers contenenti le osservazioni, potenzialmente osservate su supporti differenti.

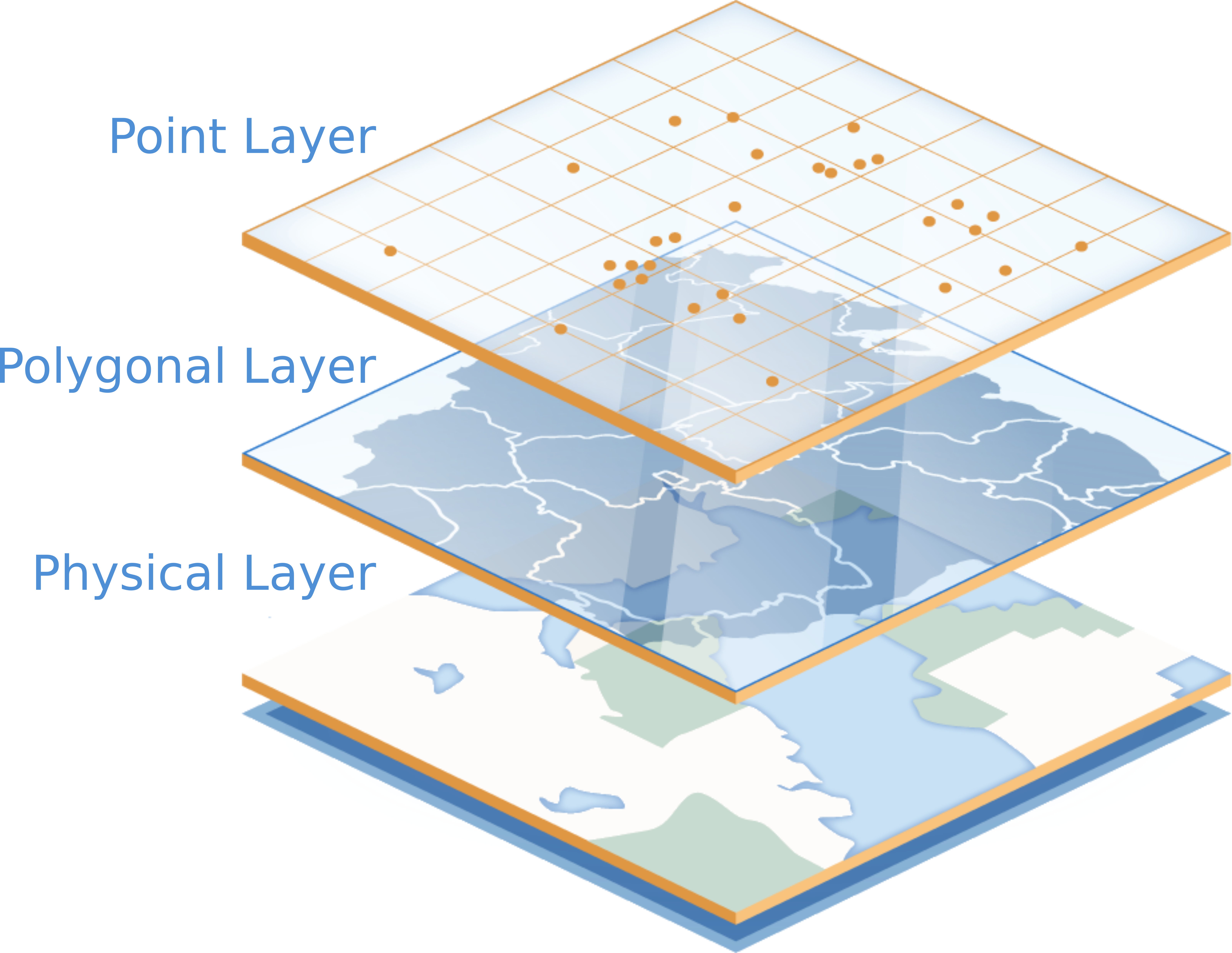
Poichè per il momento i modelli supportati gestiscono dati osservati sul medesimo supporto, i.e. sono single-layer, ed inoltre gestiscono unicamente dati scalari, ci occuperemo unicamente di questo caso.

Per aggiungere un layer scalare, ovvero in cui ad ogni locazione è associato un singolo valore numerico, si procede nel modo seguente:

1

auto& l = data.insert_scalar_layer<POINT>("layer_name", "locs.csv");

La funzione insert_sclar_layer<POINT>() inserisce un layer scalare. Per specificare che i dati sono puntuali utilizziamo il descrittore POINT. L’altro descrittore attualmente supportato è POLYGON, e definisce dati associati a poligoni, ossia quelle che per noi sono osservazioni areali.

Mentre il primo argomento di insert_sclar_layer specifica il nome simbolico del layer, il secondo argomento specifica dove i dati sono osservati. Questo può essere o il nome di un file .csv o .txt (in tal caso formattato in stile write.table) dove le coordinate sono salvate, o essere uguale al valore speciale MESH_NODES, nel qual caso i nodi della mesh sono automaticamente utilizzati come locazioni, o essere una matrice di punti definita da sorgente. Il codice seguente mostra queste ultime due casistiche:

1
2
3
4
5

auto& l = data.insert_scalar_layer<POINT>("layer_name", MESH_NODES); // observations at mesh nodes

Eigen::Matrix<double, Dynamic, Dynamic> coords;
// populate coords...
auto& l = data.insert_scalar_layer<POINT>("layer_name", coords);

Per il caso di dati areali, il seguente codice definisce un layer areale con matrice di incidenza caricata da file

1

auto& l = data.insert_scalar_layer<POLYGON>("layer_name", "incidence_mat.csv");

La matrice di incidenza è una matrice binaria che ha tante colonne quante celle della triangolazione e tante righe quante sottoregioni. L’elemento in posizione (i, j) è 1 se la cella j-esima appartiene all’i-esima sottoregione.

Dopo aver inserito le coordinate, potete procedere all’inserimento dei dati (che devono avere la stessa numerosità del numero di locazioni). Una richiesta abbastanza frequente sarà quella di caricare dati da file, operazione che può essere realizzata con il codice seguente:

1
2

l.load_csv<double>("response.csv");      // read from .csv file (you can read from .txt using load_txt)
l.load_csv<double>("design_matrix.csv");

I nomi delle colonne in questo caso sono presi dall’header dei file. Se avete dati generati da sorgente, è sempre possibile procedere come segue:

1
2
3
4
5
6

std::vector<double> vec;
l.load_vec("V1", vec);

// to load an eigen matrix
Eigen::Matrix<double, Dynamic, Dynamic> mtx;
for(int i = 0; i < mtx.cols(); ++i) { l.load_vec("V" + std::to_string(i + 1), mtx.col(i)); }

è infine possibile visualizzare il contenuto di un layer mandando l sullo stream di output

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

std::cout << l << std::endl;

                                y          x1          x2
              <POINT> <1,1:flt64> <1,1:flt64> <1,1:flt64>
(-0.925000, 0.000000)   -0.995250    0.140206   -0.798621
(-0.910947, 0.160625)    5.593103    1.198960   -0.790085
(-0.869216, 0.316369)   -2.782208   -2.329969   -0.763823
(-0.801073, 0.462500)    1.337585    0.570945   -0.718104
(-0.708591, 0.594579)    7.532907    2.748276   -0.650765
(-0.594579, 0.708591)    6.058098    1.708040   -0.560160
(-0.462500, 0.801073)   13.832988    5.952680   -0.446187
(-0.316369, 0.869216)    3.041545    0.769879   -0.311117

La struttura dati è in grado di eseguire operazioni molto più complesse, ma per questo tutorial ci limitiamo a questo caso base.

Per il caso di problemi spazio-temporali, GeoFrame è in grado di gestire arbitrarie tensorizzazioni di triangolazioni. Il codice seguente definisce un GeoFrame definito su un cilindro spazio-temporale:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// geometry
Triangulation<1, 1> T = Triangulation<1, 1>::UnitInterval(5);
Triangulation<2, 2> D(
    "mesh/nodes.csv", "mesh/cells.csv", "mesh/boundary.csv",
    /* header = */ true, /* index_col = */ true);

// data
GeoFrame data(D, T);
auto& l = data.insert_scalar_layer<POINT, POINT>("layer_name", std::pair {"locs.csv", MESH_NODES});
l.load_csv<double>("response.csv");
l.load_csv<double>("design_matrix.csv");

std::cout << l << std::endl;

                                           y          x1
              <POINT>    <POINT> <1,1:flt64> <1,1:flt64>
(-0.925000, 0.000000) (0.000000)    0.290830    0.140206
(-0.910947, 0.160625) (0.000000)    2.817051    1.198960
(-0.869216, 0.316369) (0.000000)   -5.116292   -2.329969
(-0.801073, 0.462500) (0.000000)    1.986013    0.570945
(-0.708591, 0.594579) (0.000000)    6.268801    2.748276
(-0.594579, 0.708591) (0.000000)    4.010273    1.708040
(-0.462500, 0.801073) (0.000000)   12.039375    5.952680
(-0.316369, 0.869216) (0.000000)    1.938149    0.769879

Definite le discretizzazioni temporale T e spaziale D, GeoFrame data(D, T) definisce un geoframe sul prodotto cartesiano tra D e T. In questo caso, insert_scalar_layer<POINT, POINT>() richiede due descrittori, uno per la dimensione spaziale e uno per quella temporale. Tutte le combinazioni tra POINT e POLYGON sono supportate (permettendo, ad esempio, la gestione di osservazioni puntuali in spazio e areali in tempo (<POINT, POLYGON>) o areali in spazio e puntuali in tempo (<POLYGON, POINT>)).

insert_scalar_layer richiede quindi, oltre al nome simbolico del layer, la specifica delle coordinate fisiche effettive. In questo caso, è richiesta una coppia di valori, una per la dimensione spaziale e una per quella temporale. Nell’esempio sopra, std::pair {"locs.csv", MESH_NODES} carica le locazioni spaziali da file, mentre utilizza i nodi della triangolazione T come locazioni temporali. Tutte le combinazioni di possibilità viste in precedenza sono valide.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

// geometry
Triangulation<2, 2> D = Triangulation<2, 2>::UnitSquare(100);
Triangulation<1, 1> T = Triangulation<1, 1>::UnitInterval(7);

// data
Eigen::Matrix<double, Dynamic, Dynamic> locs(500, 3);
locs.leftCols(2)  = read_csv<double>("locs_space.csv").as_matrix();
locs.rightCols(1) = read_csv<double>("locs_time.csv" ).as_matrix();

GeoFrame data(D, T);
auto& l = data.insert_scalar_layer<POINT, POINT>("layer_name", locs);

E possibile infine definire layers senza alcun dato associato. Questo può ritornare utile, ad esempio, nella definizione di problemi di processi di punto non marcati, dove non si ha nessuna quantità definita in corrispondenza della locazione. Questo è ottenuto semplicemente evitando di caricare alcun dato (tramite, e.g., read_csv o load_vec).

3. definizione della fisica:

   Tip

   Non tutte i modelli richiedono una penalizzazione, pertanto questo step è opzionale.

   a questo punto è possibile definire la fisica del problema. L’API cpp richiede sempre la definizione della fisica, anche nel caso semplice di penalizzazione laplaciana. Per definire la penalizzazione, definiamo le forme bilineari e lineari derivanti dalla formulazione debole del problema variazionale associato al problema di stima. Chiaramente, modelli diversi possono dare interpretazioni diverse a queste quantità, pertanto non esiste un ragionamento valido per ogni possible casistica. Indipendentemente dal modello statistico, l’API per la definizione di problemi differenziali permette la scrittura, e conseguente discretizzazione, di qualunque operatore differenziale, e di conseguenza, la risoluzione di qualunque PDE.

   L’API per la definizone e discretizzazione di operatori differenziali è riportata nel seguente codice:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

   FeSpace Vh(D, P1<1>); // functional space definition // trial and test function definition TrialFunction f(Vh); TestFunction v(Vh); // laplacian bilinear form auto a = integral(D)(dot(grad(f), grad(v))); // homogeneous forcing linear form ZeroField<2> u; auto F = integral(D)(u * v); // u can be any function, for instance ScalarField<2, decltype([](const Eigen::Matrix<double, Dynamic, 1>& p) { return p[0] + 2 * p[1]; // non-homoegenous forcing, here x + 2y })> u; auto F = integral(D)(u * v);

   Il primo passo è quello di definire lo spazio funzionale che vogliamo usare per discretizzare il problema differenziale. FeSpace costruisce uno spazio agli elementi finiti sulla triangolazione D, usando elementi finiti lineari scalari (significato di P1<1>). P1<N>, con N > 1, definisce uno spazio agli elementi finiti vettoriale di N componenti. Gli elementi finiti di tipo Lagrange supportati arrivano fino all’ordine P5 (anche se per i nostri interessi statistici non si andrà mai oltre P2).

   Successivamente, previa definizione delle funzioni di trial e di testing, è possibile passare alla definizione delle forme deboli. Ad esempio, la formulazione debole per un operatore di diffusione isotropa, è data come:

   \[a(f, v) = \int_{\mathcal{D}} \nabla f \cdot \nabla v\]

   e viene tradotta in codice come

   1	auto a = integral(D)(dot(grad(f), grad(v)));

   Rimando agli esempi specifici sulle PDE per esempi più avanzati.

4. definizione del modello: arrivati a questo punto, abbiamo tutti gli elementi per definire la nostra modellistica statistica. Ciascun modello ha le sue specifiche, pertanto non c’è una descrizione valida per tutti i casi.

   Prima di procedere dobbiamo introdurre Il concetto fondamentale di solver variazionale. Un solver variazionale è l’algoritmo per risolvere un problema del tipo:

   \[\begin{split}\begin{align} & \min_{\boldsymbol{f} \in \mathbb{H}} && \mathcal{F}(\boldsymbol{f}) + \mathcal{P}(\boldsymbol{f}, \boldsymbol{f}) &&\\ & \text{s.t.} && \mathcal{C}(\boldsymbol{f}) = \boldsymbol{0} \end{align}\end{split}\]

   Il problema sopra indicato è fin troppo generico. Un risolutore fissa, a meno della fisica, ovvero della penalizzazione \(\mathcal{P}(\boldsymbol{f}, \boldsymbol{f})\), tutti i dettagli che definiscono il problema variazionale, e la sua risoluzione, e.g. dettagli quali la tipologia di discretizzazione usata, l’uso o meno di un approccio misto, eventuali schemi di integrazione in tempo, etc. I risolutori sono divisi per famiglia, con al momento due famiglie disponibili:

   • ls: least square solvers: risolvono problemi del tipo

     \[\min_{f \in \mathbb{H}, \boldsymbol{\beta} \in \mathbb{R}^q} \frac{1}{n} \sum_{i=1}^n (y_i - \boldsymbol{x}_i^\top \boldsymbol{\beta} - f(\boldsymbol{p}_i))^2 + \mathcal{P}(f, f)\]

     Tra i risolutori disponibili in questa famiglia abbiamo:

     • fe_ls_elliptic(a, F): risolutore ellittico con discretizzazione agli elementi finiti. Fissa

       \[\mathcal{P}(f, f) = \int_{\mathcal{D}} (-\text{div}[K \nabla f] + \boldsymbol{b} \cdot \nabla f + cf)^2.\]

       In questo caso, a deve descrivere la forma debole dell’operatore ellittico usato nella penalizzazione, mentre F deve rappresentare la forma lineare derivante dal termine di forzante. Il perchè di questo è da ritrovarsi nell’approccio agli elementi finiti misto usato per risolvere il problema. Si rimanda alla letteratura specifica.

     • fe_ls_parabolic_mono(std::pair{a, F}, ic): risolutore spazio-tempo parabolico monolitico con discretizazzione agli elementi finiti. Fissa:

       \[\mathcal{P}(f, f) = \int_{\mathcal{D}} \Bigl(\frac{\partial f}{\partial t} -\text{div}[K \nabla f] + \boldsymbol{b} \cdot \nabla f + cf \Bigr)^2.\]

       a deve essere pari alla forma debole dell’operatore ellittico usato nella penalizzazione, mentre F rappresenta la forma lineare derivante dal termine di forzante. ic è il vettore dell’espansione in base della condizione iniziale. Il risolutore approccia il problema in maniera monolitica.

     • fe_ls_parabolic_ieul(std::pair{a, F}, ic, /* max_iter = */ 50, /* tol = */ 1e-4): risolutore spazio-tempo parabolico iterativo con discretizzazione agli elementi finiti in spazio e integrazione in tempo alla eulero implicito ieul. Risolve lo stesso problema di fe_ls_parabolic_mono ma usando un approccio diverso. A differenza di fe_parabolic_mono, prende opzionalmente in ingresso i parametri di arresto dello schema iterativo.

     • fe_ls_separable_mono(std::pair {a_D, F_D}, std::pair {a_T, F_T}): risolutore spazio-tempo separabile monolitico con discretizzazione in spazio agli elementi finiti e discretizzazione in tempo avente regolarità di sobolev maggiore di 2 (le B-Spline sono un caso specifico). Fissa

       \[\mathcal{P}(f, f) = \int_{\mathcal{D}}\int_T (L_{\mathcal{D}} f - u_{\mathcal{D}})^2 + \int_T \int_{\mathcal{D}} (L_{T} f - u_T)^2,\]

       con \(L_f\) operatore ellittico del secondo ordine in spazio e \(L_T\) operatore ellittico del secondo ordine in tempo. {a_D, F_D} sono le forme deboli per la componente in spazio, {a_T, F_T} per quella in tempo.

   • de: density estimation solvers: risolvono problemi del tipo

     \[\begin{split}\begin{aligned} & \min_{f \in \mathbb{H}} && -\frac{1}{n} \sum_{i=1}^n f(\boldsymbol{p}_i) + \mathcal{P}(f, f) &&\\ & \text{s.t.} && \int_{\mathcal{D}} e^f = 1 \end{aligned}\end{split}\]

     Tra i risolutori disponibili in questa famiglia abbiamo:

     • fe_de_elliptic(a, F): risolutore ellittico con discretizzazione agli elementi finiti. Fissa

       \[\mathcal{P}(f, f) = \int_{\mathcal{D}} (-\text{div}[K \nabla f] + \boldsymbol{b} \cdot \nabla f + cf)^2.\]

       Il significato degli argomenti è lo stesso che si ha con fe_ls_elliptic.

     • fe_de_separable(std::pair {a_D, F_D}, std::pair {a_T, F_T}): risolutore spazio-tempo separabile monolitico con discretizzazione in spazio agli elementi finiti e discretizzazione in tempo avente regolarità di sobolev maggiore di 2 (le B-Spline sono un caso specifico). Fissa

       \[\mathcal{P}(f, f) = \int_{\mathcal{D}}\int_T (L_{\mathcal{D}} f - u_{\mathcal{D}})^2 + \int_T \int_{\mathcal{D}} (L_{T} f - u_T)^2.\]

       Il significato degli argomenti è lo stesso che si ha con fe_ls_separable.

     Modelli che lo richiedono possono prendere in ingresso un solver variazionale. Ad esempio, il codice seguente:

     1	SRPDE m("y ~ f", data, fe_elliptic(a, F));

     definisce un modello di regressione spaziale non-parametrico. y nella formula (la stessa notazione di R è supportata) deve effettivamente essere un valida colonna in data. Modelli semi-parametrici possono essere gestiti manipolando la formula, ad esempio y ~ x1 + x2 + f definisce un modello che usa come covariate le colonne x1 e x2 in data.

     Modelli spazio-tempo possono essere definiti cambiando il tipo di solver variazionale, come indicato nel codice sotto:

     regressione spazio-tempo separabile¶

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

     // linear finite element in space FeSpace Vh(D, P1<1>); TrialFunction f(Vh); TestFunction v(Vh); auto a_D = integral(D)(dot(grad(f), grad(v))); ZeroField<2> u_D; auto F_D = integral(D)(u_D * v); // cubic B-splines in time BsSpace Bh(T, 3); TrialFunction g(Bh); TestFunction w(Bh); auto a_T = integral(T)(dxx(g) * dxx(w)); // bilaplacian discretization ZeroField<1> u_T; auto F_T = integral(T)(u_T * w); // modeling SRPDE m("y ~ x1 + f", data, fe_ls_separable_mono(std::pair {a_D, F_D}, std::pair {a_T, F_T}));

     regressione spazio-tempo parabolica, risolutore eulero implicito¶

     1 2 3 4 5 6 7 8 9 10 11

     vector_t ic = read_csv<double>("ic.csv").as_matrix(); // physics FeSpace Vh(D, P1<1>); TrialFunction f(Vh); TestFunction v(Vh); auto a = integral(D)(dot(grad(f), grad(v))); ZeroField<2> u; auto F = integral(D)(u * v); // modeling SRPDE m("y ~ f", data, fe_ls_parabolic_ieul(std::pair{a, F}, ic));

     Come noto, SRPDE è solo un caso specifico di regressione spaziale. Altri modelli di regressione si comportano in maniera simile, come mostrato di seguito:

     space-only non-parametric generalized regression model¶

     1 2 3 4 5 6

     GSRPDE m( "y ~ f", data, /* family = */ poisson_distribution{}, fe_ls_ellitpic(a, F) );

     space-time semi-parametric separable quantile regression model¶

     1 2 3 4 5 6

     QSRPDE m( "y ~ x1 + x2 + f", data, /* alpha = */ 0.99, fe_ls_separable_mono(std::pair {a_D, F_D}, std::pair {a_T, F_T}) );

     I modelli della famiglia di stima di densità, non prendono in ingresso una formula, essendo tutta l’informazione contenuta nelle locazioni spaziali. La loro definizione è altrettanto semplice:

     space-only density estimation model¶

     1	DEPDE m(data, fe_de_elliptic(a, F));

     space-time separable density estimation model¶

     1	DEPDE m(data, fe_de_separable(std::pair {a_D, F_D}, std::pair {a_T, F_T}));

5. fit: definito il modello, il metodo fit performa il ftting effettivo. I parametri ricevuti da fit variano da modello a modello.

   Per i metodi di regressione, fit riceve in input i parametri di smoothing (fissati). Il numero di parametri di smoothing dipende dal solver variazionale scelto (1 per problemi solo spazio, 2 per problemi spazio-tempo).

   1 2	QSRPDE m("y ~ f", data, 0.99, fe_ls_elliptic(a, F)); m.fit(1e-2);

   Modelli di stima di densità prendono in ingresso, oltre ai parametri di smoothing, il punto iniziale dell’ottimizzazione insieme all’algoritmo di ottimizzazione utilizzato per la minimizzazione del funzionale:

   1 2 3 4 5 6

   DEPDE m(data, fe_de_elliptic(a, F)); m.fit( /* lambda = */ 0.1, g_init, /* optimizer = */ GradientDescent<Dynamic, BacktrackingLineSearch> {1000, 1e-5, 1e-2} );

   Usare BFGS<Dynamic> come ottimizzatore avrebbe forzato la risoluzione del problema di stima di densità tramite BFGS, etc.etc.

7. export dei risultati: infine i risultati possono essere scritti su file per poi essere caricati, ad esempio, su R. Per esportare un file in formato csv, è sufficiente utilizzare la seguente linea di codice:

   1	write_csv("log_density.csv", m.log_density()); // save estimated log density in file log_density.csv

Se sei arrivato fin qui significa che sei ben motivato! Questo mostra un uso molto basic dell’API di fdaPDE. In realtà, puoi sviluppare modelli ben più sofisticati a partire dalla sola API esterna (vale a dire, senza scendere in cantina)!!

Se hai domande, sai come trovarmi :)

Di seguito trovate degli script completi di esempio:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#include <fdaPDE/models.h>
using namespace fdapde;

int main() {

   // geometry
   Triangulation<2, 2> unit_square = Triangulation<2, 2>::UnitSquare(10);
   // mark left side of square (where we will impose non-homegenous Neumann BCs) with 1
   unit_square.mark_boundary(/* as = */ 1, /* where = */ [](const auto& edge) {
      return (edge.node(0)[0] == 0 && edge.node(1)[0] == 0);
   });

   // data
   GeoFrame gf(unit_square);
   auto& l = gf.add_scalar_layer<POINT>("layer", MESH_NODES);
   l.load_csv<double>("response.csv");

   // physics
   FeSpace Vh(unit_square, P1<1>);
   TrialFunction f(Vh);
   TestFunction  v(Vh);
   // anysotropic diffusion tensor
   Eigen::Matrix<double, 2, 2> K;
   K << 2, 1, 1, 4;
   // neumann data
   ScalarField<2, decltype([](const Eigen::Matrix<double, 2, 1>& p) {
       return p[1] * (1 - p[1]);
   })> g_N;
   // homogeneous forcing field
   ZeroField<2> u;
   auto a = integral(unit_square)(dot(K * grad(f), grad(v)));
   auto F = integral(unit_square)(u * v) + integral(unit_square.boundary(/* on = */ 1))(g_N * v);

   // modeling
   SRPDE m("y ~ f", gf, fe_ls_elliptic(a, F));

   // calibration
   std::vector<double> lambda_grid = {1e-4, 1e-3, 1e-2, 1e-1};
   GridOptimizer<1> opt;
   opt.optimize(m.gcv(), lambda_grid);

   // fit at optimal smoothing level
   m.fit(opt.optimum());

   // export
   write_csv("estimate.csv", m.f());

   return 0;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include <fdaPDE/models.h>
using namespace fdapde;

int main() {
   using matrix_t = Eigen::Matrix<double, Dynamic, Dynamic>;
   using vector_t = Eigen::Matrix<double, Dynamic, 1>;

   // geometry
   Triangulation<2, 2> unit_square = Triangulation<2, 2>::UnitSquare(10);

   // data
   vector_t ic = read_csv<double>("ic.csv").as_matrix();
   GeoFrame gf(unit_square);
   auto& l = gf.add_scalar_layer<POLYGON>("layer", "incidence_mtx.csv");
   l.load_csv<double>("response.csv");

   // physics
   FeSpace Vh(unit_square, P1<1>);
   TrialFunction f(Vh);
   TestFunction  v(Vh);
   // read operator coefficients from file
   FeCoeff<2, 2, 2, matrix_t> K(read_csv<double>("diffusion.csv").as_matrix());
   FeCoeff<2, 2, 1, matrix_t> b(read_csv<double>("transport.csv").as_matrix());
   // homogeneous forcing field
   ZeroField<2> u;
   auto a = integral(D)(dot(K * grad(f), grad(v)) + dot(b, grad(f)) * v);
   auto F = integral(unit_square)(u * v);

   // modeling
   SRPDE m("y ~ f", gf, fe_ls_parabolic_mono(std::pair{a, F}, ic));

   // calibration
   std::vector<double> lambda_grid = {1e-4, 1e-3, 1e-2, 1e-1};
   GridOptimizer<1> opt;
   opt.optimize(m.gcv(), lambda_grid);

   // fit at optimal smoothing level
   m.fit(opt.optimum());

   // export
   write_csv("estimate.csv", m.f());

   return 0;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include <fdaPDE/models.h>
using namespace fdapde;

int main() {
   using matrix_t = Eigen::Matrix<double, Dynamic, Dynamic>;
   using vector_t = Eigen::Matrix<double, Dynamic, 1>;

   // geometry
   std::string mesh_path = "...";
   Triangulation<2, 2> D(
       mesh_path + "points.csv", mesh_path + "elements.csv", mesh_path + "boundary.csv", true, true);
   Triangulation<1, 1> T = Triangulation<1, 1>::UnitInterval(7);

   // data
   Eigen::Matrix<double, Dynamic, 1> g_init = read_csv<double>("f_init.csv").as_matrix().array().log();
   matrix_t locs(500, 3);
   locs.leftCols(2)  = read_csv<double>("../data/de/03/data_space.csv").as_matrix();
   locs.rightCols(1) = read_csv<double>("../data/de/03/data_time.csv" ).as_matrix();
   GeoFrame data(D, T);
   auto& l1 = data.insert_scalar_layer<POINT, POINT>("l1", locs);

   // physics
   FeSpace Vh(D, P1<1>);   // linear finite element in space
   TrialFunction f(Vh);
   TestFunction  v(Vh);
   auto a_D = integral(D)(dot(grad(f), grad(v)));
   ZeroField<2> u_D;
   auto F_D = integral(D)(u_D * v);

   BsSpace Qh(T, 3);   // cubic B-spline in time
   TrialFunction g(Qh);
   TestFunction  w(Qh);
   auto a_T = integral(T)(dxx(g) * dxx(w));
   ZeroField<1> u_T;
   auto F_T = integral(T)(u_T * w);

   // modeling
   DEPDE m(data, fe_de_separable(std::pair {a_D, F_D}, std::pair {a_T, F_T}));
   m.fit(0.00025, 0.01, g_init, BFGS<Dynamic> {100, 1e-5, 1e-2});

   // export
   write_csv("estimate.csv", m.log_density());

   return 0;
}